A Fractional Order Numerical Study for the Influenza Disease Mathematical Model

By Salem Ben Said, Zulqurnain Sabir and Qasem Al-Mdallal

Department of Mathematical Sciences, College of Sciences

Published in Alexandria Engineering Journal (2023) volume 65, 615-626

The purpose of this work is to find the numerical solutions of the fractional order mathematical influenza disease model by designing the computational frameworks based on the Levenberg-Marquardt backpropagation neural networks. The fractional order derivatives have been used to get more accurate performances of the mathematical influenza disease model as compared to the integer order derivatives. There are various deterministic or conventional schemes that have been applied to present the numerical performances of the mathematical form of the influenza disease model, but the stochastic structure using the Levenberg-Marquardt backpropagation neural networks has never been implemented before to solve the mathematical influenza disease model, which depends upon the fractional order nonlinear system of differential equations. The flowchart of the SIRC model is illustrated in Figure below.

 

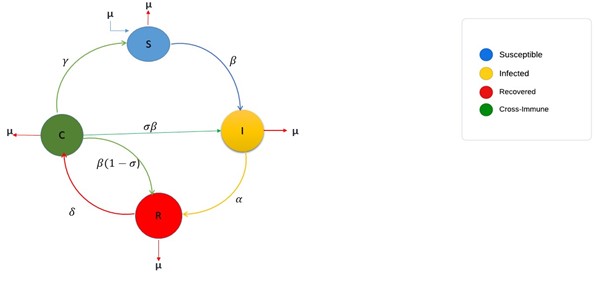
Figure: General flow diagram of the model

The mathematical model shows that after recovery from infection, the individuals enter a new class C. More precisely, the individuals in R class are those who have recovered from the dominant strain currently circulating and against which they have full immunity. Then, after some period, the individuals move to C class, because they have only partial immunity to a new dominant strain that has emerged since they were last infected. Thus, the movements of individuals among different immune classes are caused by the fact that the moving frame in immune space is implemented, exactly as in Pease’s approach. While in the compartment C, the individuals are exposed to the currently dominant strain at the same contact rate  of the susceptible S.

The results have been achieved with input [0, 1] and 0.01 step size. The best values The methodology is based on the dataset for different variants of the model, which is generated by the reference Adams method that is a built-in solver in the Mathematica package. In this command ‘Adams’ is applied by using the default setting of the parameter for implementation and termination tolerances. The obtained results have been used as a target and the testing, training and authentication procedure is applied by using the Levenberg-Marquardt backpropagation neural networks. Fifteen number of neurons together with the statics of training are selected as 78%, while for both authentication and testing measures have been chosen as 11%. The different values of these samples can also be selected. If the selection of the training values is > 78%, then the better performances can be achieved because of the bias input values. Moreover, the data for the training samples is < 78%, then the accurateness of the scheme is degraded considerably for solving the model. Hence, the sample data for the unbiased and bias inputs should be adjusted with concentration to avoid both divergence and premature convergence. The stochastic procedures are authenticated through the software ‘Matlab’ by applying the appropriate learning scheme, log-sigmoid activation function, authorization matrices, Levenberg-Marquardt backpropagation optimization scheme, hidden neurons, and testing data.of the obtained performances, gradient, error histograms have been presented at Epochs 96, 66, and 61 for solving the fractional order disease model. The correctness of the scheme is observed through the comparison of the results along with the absolute error values. It is observed that the obtained and proposed results overlapped with each other, which perform the exactness of the designed stochastic scheme. Moreover, the negligible absolute error in each case of the model presents the accuracy and precision of the stochastic scheme. It is also observed that the parameter µ, which represents the mortality rate in every compartment and is assumed to equal the rate of newborns in the population (because population size is assumed to be constant) that is supposed to be susceptible individuals. Its inverse, i.e., can be easily adjusted as the average lifetime of human hosts. The parameters  and are the inverses of the average time spent by the individuals in three compartments I, R and C, respectively. While the value of the infectious period can be estimated based on clinical observations only and these values vary between 2 and 7 days of flu.

This work has been performed by the joint efforts of Dr. Zulqurnain Sabir, Dr. Salem Ben Said, and Prof. Qasem Al-Mdallal. Dr. Zulqurnain Sabir proposed the idea and solved the model, Prof. Qasem Al-Mdallal helped to adjust the values of the fractional order and carefully noticed the results, while Dr. Salem Ben Said supervised the entire work and helped in writing the paper. Moreover, the first author is working in the United Arab Emirates university as a senior researcher with Dr. Salem Ben Said.