أخبار البحث العلمي

دراسة النموذج الرياضي العددي ذو الترتيب الجزئي لمرض الإنفلونزا

إعداد د. سالم بن سعيد ود. ذوالقرنين صابر و د. قاسم المدلل

من قسم علوم الرياضيات في كلية العلوم

نُشر في مجلة كلية الهندسة جامعة الإسكندرية (2023) المجلد 65 ، 615-626

يهدف هذا البحث إلى إيجاد الحلول العددية للنموذج الرياضي ذو الرتب الجزئية (ذو الترتيب الجزئي) لمرض الإنفلونزا من خلال تصميم الأطر الحسابية بناء على الانتشار الخلفي لشبكات ليفنبرغ ماركوارت العصبية الإرجاعية Levenberg-Marquardt backpropagation. وتم استخدام مشتقات الرتب الجزئية للحصول على أداء أكثر دقة لنموذج مرض الإنفلونزا الرياضي مقارنة بمشتقات الترتيب الصحيح. ولعرض الأداء العددي للشكل الرياضي لنموذج مرض الإنفلونزا فقد تم تطبيق العديد من المخططات المحددة أو التقليدية، ولكن لم يسبق وأن تم تنفيذ الهيكل العشوائي باستخدام الانتشار الخلفي لشبكات ليفينبيرغ ماركوارت العصبيةLevenberg-Marquardt backpropagation لحل النموذج الرياضي لمرض الإنفلونزا، والتي تعتمد على نظام المعادلات التفاضلية الجزئية غير الخطية. الرسم البياني أدناه يوضح نموذج SIRC.

 

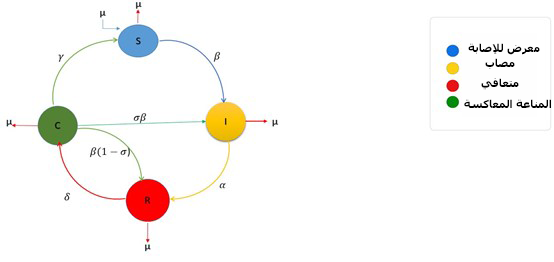
الشكل: مخطط تدفق البيانات للنموذج

يوضح النموذج الرياضي أنه بعد التعافي من العدوى يدخل الأشخاص فئة جديدة C. وبتعبير أكثر دقة، فإن الأشخاص في الفئة R هم أولئك الذين تعافوا من السلالة السائدة المنتشرة حاليًا والتي لديهم مناعة كاملة ضدها. ثم بعد فترة بسيطة ينتقلون إلى الفئة C، لأن لديهم مناعة جزئية فقط لسلالة سائدة جديدة ظهرت منذ أن أصيبوا آخر مرة، لذلك فإن تحركات الأشخاص بين الفئات المناعية المختلفة ناتجة عن حقيقة تطبيق الإطار المتحرك في الفضاء المناعي، تمامًا كما هو الحال في طريقة بيزPease. وعند وجود الأشخاص في الفئة C فإنهم يتعرضون للسلالة السائدة حاليًا بنفس معدل تلامس β من S.

وتعتمد المنهجية على مجموعة بيانات لمتغيرات مختلفة للنموذج، والتي يتم إنشاؤها بواسطة طريقة Adams المرجعية التي تعد وسيلة حل مضمنة في حزمة Mathematica. ويتم تطبيق "Adams" باستخدام الإعداد الافتراضي لمعامل التفاوتات في التنفيذ والإنهاء، ولقد استخدمت النتائج التي تم الحصول عليها كهدف، ويتم تطبيق إجراءات الاختبار والتدريب والمصادقة باستخدام شبكات ليفنبيرغ ماركوارت العصبية backpropagation Levenberg-Marquardt. تم اختيار خمسة عشر عددًا من الخلايا العصبية إلى جانب إحصائيات التدريب بنسبة 78٪، بينما تم اختيار 11% من إجراءات المصادقة والاختبار. ويمكن أيضًا اختيار القيم المختلفة لهذه العينات، إذا كان اختيار قيم التدريب > 78٪ ، فيمكن تحقيق الأداء الأفضل بسبب قيم إدخال التحيز، علاوة على ذلك، فلقد بلغت بيانات عينات التدريب <78٪، وبذلك تقل دقة النظام بشكل كبير لحل النموذج، بالإضافة إلى أنه يجب التركيز عند تعديل بيانات العينة للمدخلات غير المتحيزة والمتحيزة لتجنب كل من التباعد والتقارب المبكر. وللتحقق من صحة الإجراءات العشوائية يستخدم برنامج "Matlab" من خلال تطبيق مخطط التعلم المناسب، وتابع سيغمويد sigmoid أو تابع التفعيل اللوجستي، ومصفوفات التفويض، ومخطط تحسين خوارزمية الانتشار الخلفيLevenberg-Marquardt backpropagation، والخلايا العصبية المخفية، وبيانات الاختبار.

تم تحقيق النتائج مع المدخلات [0،1] وحجم خطوة 0.01. أفضل القيم تم الحصول عليها للأداء، والانحدار والمدرج التكراري الخطأ في العصور 96 و66 و61 لحل نموذج مرض الرتبة الجزئية. يتم ملاحظة صحة المخطط من خلال مقارنة النتائج مع قيم الخطأ المطلقة. ويلاحظ أن النتائج التي تم الحصول عليها والمقترحة تتداخل مع بعضها البعض، مما يؤدي إلى دقة المخطط العشوائي المصمم. علاوة على ذلك، فإن الخطأ المطلق الذي لا يكاد يذكر في كل حالة من حالات النموذج يعرض دقة المخطط العشوائي. ويلاحظ أيضًا أن المعامل µ، الذي يمثل معدل الوفيات في كل قسم، ويفترض أنه يساوي معدل المواليد الجدد في السكان (لأنه من المفترض أن يكون حجم السكان مطرداّ) والذي من المفترض أن يكونوا أفرادًا معرضين للإصابة. يمكن تعديل معكوسها، أي µ ^ (- 1) بسهولة كمتوسط عمر المضيف البشري. المعاملات α و و  هي انعكاسات متوسط الوقت الذي يقضيه الأفراد في ثلاثة أقسام I و R و C على التوالي. في حين أن قيمة الفترة المعدية   يمكن تقديرها بناءً على الملاحظات السريرية فقط وتختلف هذه القيم بين 2 و 7 أيام من الإنفلونزا.

تم تنفيذ هذا العمل بجهود مشتركة للدكتور ذو القرنين صابر والدكتور سالم بن سعيد والأستاذ الدكتور قاسم المدلل. طرح الدكتور ذو القرنين صابر الفكرة وحل النموذج، وساعد الأستاذ الدكتور قاسم المدلل على تعديل قيم الكسر ولاحظ النتائج بعناية، بينما أشرف الدكتور سالم بن سعيد على العمل بأكمله وساعد في كتابة الورقة. ويعمل المؤلف الأول في جامعة الإمارات العربية المتحدة كباحث أول مع الدكتور سالم بن سعيد.